|
№1. Док-те неравенство Коши.
Если a1, ... , an > 0, то
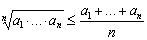
Вспомогательная лемма:
если произведение n положительных чисел равно 1, то их сумма больше или равна n.
Пусть a1, ... , an > 0, причём a1*...*an = 1. Тогда a1+...+an ≥ n.
Докажем по индукции:
База: при n=1 утверждение очевидно
Шаг: пусть утверждение верно для n=k, т.е. a1*...*ak=1 => a1+...+ak ≥ k. Заметим, что
среди чисел a1, ... , ak найдётся пара (для определённости a1, a2) такая, что
a1≥1, a2≤1:
(a1-1)(a2-1) ≤ 0
a1*a2+1 ≤ a1+a2
Пусть теперь имеется (k+1) число, тогда a1*...*ak+1 = 1. Мы хотим док-ть, что a1+...+ak+1 ≥ k+1. Как
уже было показано, из a1, ... , ak+1 найдутся два числа такие, что
a1*a2+1 ≤ a1+a2
Прибавим к обеим частям этого неравенства a3+...+ak+1. Получим
a1+...+ak+1 ≥ a1*a2+a3+...+ak+1+1 ≥ k+1,
где a1*a2+a3+...+ak+1 - сумма k чисел, произведение которых равно 1
Теперь докажем неравенство Коши. Пусть a1*...*an = А. Тогда
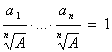
По вспомогательной лемме получаем:
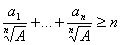
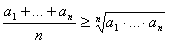
№2. Известно, что некоторый многочлен в рациональных точках принимает рациональные значения. Док-те,
что все его коэффициенты рациональны.
Пусть F(x)=aoxn+a1xn-1+...+an-1x1+anx0.
Тогда x є Q, F(x) є Q => ai є Q, где i = 0, 1, ... , n
Проведём доказательство по индукции
База: n=0: F(x)=ao, F(x) є Q => ao є Q
Шаг: Пусть утв. верно при k ≥ 0, т.е.
Fk(x)=aoxk+a1xk-1+...+ak-1x1+akxo
x є Q, Fk(x) є Q => ai є Q, где i = 0, 1, ... , k
Покажем, что верно
Fk+1(x)=aoxk+1+a1xk+...+akx1+ak+1xo
x є Q, Fk+1(x) є Q => ai є Q, где i = 0, 1, ... , k+1
Действительно,
Fk+1(x)=xFk(x)+ak+1,
где Fk(x), Fk+1(x), x є Q => ak+1 є Q
№3. Док-те, что если 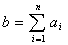 и d|ai, где i=1, 2, ... , n, то d|b. и d|ai, где i=1, 2, ... , n, то d|b.
Согласно условию
ai=dqi
b=a1+a2+...+an=dq1+dq2+...+dqn=d(q1+q2+...+qn)=dq'
Отсюда получаем: d|b
№4. Док-те, что если a и b - целые взаимно простые числа, то ур-ние ax+by=1 разрешимо в целых числах.
Ясно, что можно считать, что a, b є N.
Будем док-ть с помощью индукции по величине суммы a+b=n.
База: a+b=2 => a=b=1. Решением ур-ния является, например, пара (0,1)
Шаг: предположим истинность утв. для всех пар (a,b)=1 с суммой a+b<k (k>2). Покажем, что тогда утв. справедливо и для пар
a и b таких, что (a,b)=1 и a+b≤k
Рассмотрим два случая:
1) (a,b)=1, a+b<k - утв. верно по предположению;
2) (a,b)=1, a+b=k
Без ограничения общности будем считать, что a>b. Тога (a-b,b)=1 и к тому же (a-b)+b=a<k. Тогда по предположению
ур-ние
(a-b)U+bV=1 разрешимо в целых числах. Тогда
aU+b(V-U)=1 также разрешимо в целых числах
или ax+by=1
№5. Док-те, что если a, b и c - целые числа, причём (a,b)=1 и b|ac, то b|c
b|ac => ac=bq
Поскольку (a,b)=1, то c=b(q/a)=bq' => b|c
№6. Док-те, что наименьший отличный от 1 делитель натурального числа n>1 есть простое число
Пусть q≠1 - наименьший делитель некоторого натурального числа n>1. Предположим, что q-составное, т.е.
q=ab, где 1<a<q, 1<b<q
Но тогда по одной из лемм: q|n, a|q => a|n. К тому же a<q => a - наименьший делитель n. Полученное противоречие завершает
док-во: q-простое
№7. Док-те, что наименьший простой делитель составного числа n не превосходит 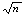 . .
Пусть q-наименьший ≠1 делитель числа n. Тогда q-простое. При этом n=qa, где a≥q. Следовательно
aq≥q2 => n≥q2 => 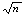 ≥q ≥q
№8. Док-те, что если p-простое число, то любое целое число a либо взаимно просто с p, либо делится на p
Поскольку, p-простое число, тогда
либо (a,p)=1 => a взамно просто с p;
либо (a,p)=p => a делится на p
№9. Док-те, что 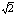 является иррациональным числом является иррациональным числом
Предположим, что 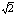 - рациональное число, т.е. - рациональное число, т.е.
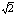 = a/b. Можем считать, что все сокращения произведены и числа a и b не имеют общих
множителей. Возводя в квадрат это соотношение, получаем: = a/b. Можем считать, что все сокращения произведены и числа a и b не имеют общих
множителей. Возводя в квадрат это соотношение, получаем:
2b2 = a2
По теореме о единственности разложения число a делится на 2, следовательно, a2 делится на 4. И вновь по теореме о единственности разложения,
применённой к числу b2, получаем, что b делится на 2, что противоречит предположению о том, что числа a и b не имеют общих
множителей. Полученное противоречие показывает, что 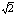 - число иррациональное. - число иррациональное.
О. Оре 'Приглашение в теорию чисел' (стр. 122-123)
№10. Док-те, что при n>1 справедлива формула
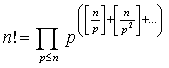 , ,
где произведение берётся по всем простым числам, не превосходящим числа n.
Нам необходимо найти наибольшую степень числа p, на которую делится n!. Каждое p-ое число: p, 2p, 3p, ... - делится на p.
Всего таких чисел, не превосходящих числа n, [n/p]. Однако некоторые из них делятся на вторую степень числа p, а именно:
p2, 2p2, 3p2, ... . Таких чисел существует [n/p2]. Некоторые из них делятся на третью степень числа p
, т.е. на p3: p3, 2p3, 3p3, ... - их существует [n/p3] и т.д.
Это показывает, что выражение для точной степени числа p, делящей число n! таково:
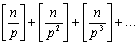
Таким образом,
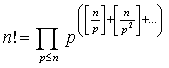 , ,
где произведение берётся по всем простым числам, не превосходящим числа n.
№11. Пусть каноническое разложение числа n имеет вид
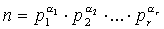
Док-те, что число его делителей: 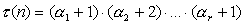
Если число d является делителем числа n, т.е. n=dd1, то единственными простыми числами, на которые может
делиться число d, будут только те, которые делят число n, а именно: p1, ... , pr. Таким образом,
мы можем записать разложение числа d на простые множители в виде

Простое число p1 может содержаться не более 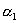 раз, как
и в самом числе n; аналогично - для p2 и других простых чисел. Это значение для числа раз, как
и в самом числе n; аналогично - для p2 и других простых чисел. Это значение для числа 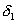 мы можем выбрать
мы можем выбрать 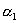 +1 способом: +1 способом: 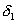 =0, 1, ... , =0, 1, ... , 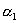 .
Аналогично и для других простых чисел. Так как каждое из .
Аналогично и для других простых чисел. Так как каждое из 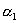 +1 значений,
которые может принимать число +1 значений,
которые может принимать число 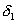 , может сочетаться с любым из , может сочетаться с любым из 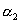 +1
возможных значений числа +1
возможных значений числа 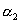 и т.д., то мы видим, что общее число делителей числа n задаётся формулой и т.д., то мы видим, что общее число делителей числа n задаётся формулой
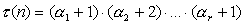
№12. Док-те, что 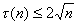
n=d1d2
Пусть d1≤d2. Тогда d1≤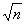 ≤d2. Отсюда
все делители числа n разбиваются на две группы - меньшие и большие корня из n. Причём каждому делителю из 1ой группы соответствует делитель из
2ой группы и наоборот. Пусть D1 и D2 кол-во делителей в каждой из групп (D1=D2). Тогда ≤d2. Отсюда
все делители числа n разбиваются на две группы - меньшие и большие корня из n. Причём каждому делителю из 1ой группы соответствует делитель из
2ой группы и наоборот. Пусть D1 и D2 кол-во делителей в каждой из групп (D1=D2). Тогда
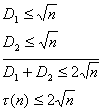
№13. Док-те, что существуют сколь угодно длинные отрезки натурального ряда, не содержащие ни одного простого числа
При n>2 (n є N): Nk=n!+k, k=2, 3, ... , n
Числа Nk представляют собой (n-1) последовательно идущих натуральных чисел, при этом все они составные, поскольку k|Nk
№14. Док-те, что при n>2 между n и n! содержится по крайней мере одно простое число
Предположим обратное.
Пусть p1, ... , pk - все простые числа ≤n. Возъмём число N=p1...pk+1.
Видно, что n<N<n!, причём N-простое число. Полученное противоречие завершает док-во: мы нашли простое число между n и n!
№15 - №21. Сравнения. Леммы
Для док-ва используем определение сравнения: a ≡ b (mod m) <=> a=mq1+r, b=mq2+r <=> a-b=mq
№22. Док-те, что если a2+b2 делится на 3, то a и b оба делятся на 3
Поскольку 3|(a2+b2), то можно рссмотреть две возможные ситуации:
1) 3|a => 3|b;
2) a не делится на 3: рассмотрим разные представления чисел a и b:
2.1) a=3k+1, b=3n+1
2.2) a=3k+1, b=3n+2
2.3) a=3k+2, b=3n+2
как нетрудно заметить, сумма квадратов a2+b2 во всех трёх случаях (2.1, 2.2, 2.3) не делится на 3
№23. Док-те, что все числа Ферма (Fn = 22n+ 1), начиная с n = 2, оканчиваются цифрой 7.
22n+ 1 ≡ 7 (mod 10)
22n ≡ 6 (mod 10)
Докажем по индукции:
База: n=2 22n ≡ 6 (mod 10) - истина
Шаг: предположим истинность утверждения при k ≥ 2:
22k ≡ 6 (mod 10) (*)
Покажем, что верно:
22k+1 ≡ 6 (mod 10)
Возведём (*) в квадрат:
22k+1 ≡ 36 ≡ 6 (mod 10)
№24. Док-те, что если a и b - взаимно простые целые числа, то каждый простой нечётный делитель числа a2+b2
имеет вид 4n+1.
Пусть p - простой нечётный делитель a2+b2. Тогда
a2 ≡ -b2 (mod p)
Причём p не делит ни a, ни b.
Возведём сравнение в степень (p-1)/2:
ap-1 ≡ 1 (mod p)
bp-1 ≡ 1 (mod p)
Тогда 1 ≡ (-1)(p-1)/2 (mod p). Следовательно
(p-1)/2 = 2n => p=4n+1
№25. Док-те, что существует бесконечно много простых чисел вида 4n+3
Пусть утв. неверно и p1, p2, ... , pr - все простые вида 4n+3
Рассмотрим число N=4p1p2...pr-1 - это число вида 4n+3, оно нечётное.
Следовательно, все его простые делители - нечётные числа, которые могут иметь вид либо 4n+1, либо 4n+3.
Произведение чисел вида 4n+1 есть число того же вида => у числа N имеется простой делитель вида 4n+3. Обозначим его
за p. Очевидно, что p≠pi, i=1, 2, ... , r => есть ещё одно простое число вида 4n+3
№26. Док-те, что существует бесконечно много простыхчисел вида 6n+5
Предположим, что простых чисел вида 6n+5 конечное число: p1, p2, ... , pr.
Рассмотрим число N=6p1p2...pr-1. Это число вида 6n+5.
Произведение чисел вида 6n+1 есть число того же вида => у числа N имеется простой делитель вида 6n+5 (или 6n-1=6n-1+6-6=6(n-1)+5).
Обозначим его через p. Очевидно, что p≠pi, i-1, 2, ... , r => есть ещё одно простое число вида 6n+5
№27. Док-те, что существует бесконечно много простых чисел вида 4n+1
Пусть утв. неверно: p1, ... , pr - все простые вида 4n+1
Рассмотрим N=(2p1p2...pr)2+1=a2+b2
Данное число имеет простой делитель вида 4n+1. Этот делитель будет очевидно отличен от p1, ... , pr.
№28. Док-ть, что натуральное число n делится на 3 (на 9) тогда и только тогда, когда на 3 (на 9) делится сумма его цифр
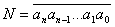 , ai-цифры, an≠0 , ai-цифры, an≠0
N=an*10n+an-1*10n-1+...+a1*10+a0
Пусть сумма an+an-1+...+a1+a0 делится на 3. Тогда (99..99+1)an+(99..99+1)an-1+...+(9+1)a1+a0=
=9(11..11an+11..11an-1+...+a1)+an+an-1+...+a1+a0, т.е. 3|N
№29. Док-ть, что для того, чтобы натуральное число n делилось на 11, необходимо и достаточно, чтобы разность сумм цифр,
стоящих на чётных и нечётных местах в записи данного числа, делилась на 11.
1 ≡ 1 (mod 11)
10 ≡ -1 (mod 11)
100 ≡ 1 (mod 11)
1000 ≡ -1 (mod 11)
И вообще
102n ≡ 1 (mod 11)
102n+1 ≡ -1 (mod 11)
1, -1, 1, -1 - характеристический ряд модуля 11
N=an*10n+an-1*10n-1+...+a1*10+a0 ≡ (-1)nan+(-1)n-1an-1+...-a1+a0 (mod 11)
№30. Док-те, что корень n-ой степени из единицы ε тогда и только тогда будет первообразным, когда его степени
εk, k=0,1, ... , k-1, различны
Если все степени εk различные, то ε-первообразный корень
Пусть теперь ε-первообразный корень, εk=εm, где k≥0, m≥0, m≤n-1, k≠m.
Пусть для определённости k>m. Тогда
εk-m=εk/εm=1 => ε-не может быть первообразным
№31. Док-те, что если ε етсь первообразный корень n-ой степени из единицы, то εk
тогда и только тогда является первообразным корнем n-ой степени из единицы, когда (k, n)=1
Пусть ε-первообразный корень n-ой степени из единицы, (k, n)=d
Пусть d>1. Тогда k=dk1, n=dn1
(εk)n1=εdk1n1=(εn)k1=1 => εk-не является первообразным
Пусть d=1, εk-корень m-ой степени из единицы, где m<n. Тогда
(εk)m=εkm=1, а т.к. εn=1, то n|km
Такого быть не может, т.к. (k,n)=1, m<n. Противоречие с предположением о том, что существует m<n: (εk)m=1
№32. Найдите сумму и произведение всех корней n-ой степени из единицы (n>1)
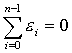 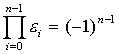
Док-во с помощью следующего утв.: все корни n-ой степени из единицы явл. вершинами правильного n-угольника, вписанного в ок-сть
№33. Док-те, что 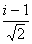 -первообразный корень 8-й степени из единицы -первообразный корень 8-й степени из единицы
εk-первообразный <=> (k,n)=1
(k,8)=1 => k=1,3,5,7
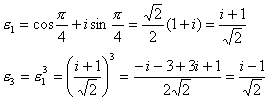
|
